| 6/7/2024 |
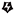 is the energy symbol. It represents one energy counter. is the energy symbol. It represents one energy counter. |
| 6/7/2024 |
Energy counters are a kind of counter that a player may have. They're not associated with any specific permanents. |
| 6/7/2024 |
Keep track of how many energy counters each player has. Potential ways to track this include writing theme down on paper or using dice, but any method that is clear and mutually agreeable is fine. (At higher levels of tournament play, dice may not be allowed for tracking counters that players have.) |
| 6/7/2024 |
If an effect says you get one or more 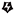 , you get that many energy counters. To pay one or more , you get that many energy counters. To pay one or more 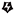 , you lose that many energy counters. You can't pay more energy counters than you have. Any effects that interact with counters a player gets, has, or loses can interact with energy counters. , you lose that many energy counters. You can't pay more energy counters than you have. Any effects that interact with counters a player gets, has, or loses can interact with energy counters. |
| 6/7/2024 |
Energy counters aren't mana. They don't go away as steps, phases, and turns end, and effects that add mana "of any type" can't give you energy counters. |
| 6/7/2024 |
Some triggered abilities state that you "may pay" a certain amount of 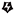 . You can't pay that amount multiple times to multiply the effect. You simply choose whether or not to pay that amount of . You can't pay that amount multiple times to multiply the effect. You simply choose whether or not to pay that amount of 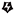 as the ability resolves. as the ability resolves. |
| 6/7/2024 |
Some triggered abilities that state that you "may pay" a certain amount of 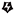 describe an effect that happens "If you do." In that case, no player may take actions to try to stop the ability's effect after you make your choice. If the payment is followed by the phrase "When you do," then you'll choose any targets for that reflexive triggered ability and put it on the stack before players can take actions. describe an effect that happens "If you do." In that case, no player may take actions to try to stop the ability's effect after you make your choice. If the payment is followed by the phrase "When you do," then you'll choose any targets for that reflexive triggered ability and put it on the stack before players can take actions. |
| 6/7/2024 |
If a spell or ability with one or more targets states that you "may pay" some amount of 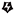 , and each permanent that it targets has become an illegal target, the spell or ability won't resolve. You can't pay any , and each permanent that it targets has become an illegal target, the spell or ability won't resolve. You can't pay any 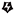 even if you want to. even if you want to. |
| 6/7/2024 |
Some spells and abilities that give you 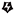 may require targets. If each target chosen is an illegal target as that spell or ability tries to resolve, it won't resolve. You won't get any may require targets. If each target chosen is an illegal target as that spell or ability tries to resolve, it won't resolve. You won't get any 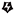 . . |
|