| 1/22/2016 |
You cast the card during the resolution of the enters-the-battlefield ability, not later in the turn. If it's a sorcery card, ignore the timing restrictions based on it being a sorcery card. Other timing restrictions, such as "Cast [this card] only during combat," must be followed. |
| 1/22/2016 |
If you can't cast the target instant or sorcery card, perhaps because there are no legal targets available, or if you choose not to cast it, it will remain in your graveyard. |
| 1/22/2016 |
If you cast a card "without paying its mana cost," you can't pay alternative costs such as surge costs. You can pay additional costs. If the card has mandatory additional costs, you must pay those. |
| 1/22/2016 |
If the instant or sorcery card has 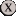 in its mana cost, you must choose 0 as its value. in its mana cost, you must choose 0 as its value. |
| 1/22/2016 |
If an instant or sorcery card you cast this way is countered, it will be exiled. |
| 1/22/2016 |
If an instant or sorcery card you cast this way goes to a zone other than exile or a graveyard, perhaps because one of its abilities says to put it into its owner's hand, it won't be exiled. This is true even if the card would be put into a graveyard later that turn. |
|